杂志文章

本文摘自《创造》杂志中文版第40卷第4期

* 本文是一篇同名文章的摘选，作者在原文中的讨论范围更加广泛，引证更加丰富。读者可以在以下网址看到这篇文章（creation.com/euler）。

莱昂哈德·欧拉（Leonhard Euler）是史上最伟大的数学家和理论物理学家之一，著作极多。他几乎在数学的纯理论与应用层面都有贡献——在微积分、数论、记数法、光学、天体力学、理论力学和流体力学领域尤为突出。¹

他将数学运用到实际问题上，在制图学、年代学、船舶建造、桥梁建设和弹道学取得许多实际成果。这些成就也让他位居阿基米德、牛顿和高斯之列。瑞士著名的科学历史学家埃米尔·费尔曼评价欧拉“迄今不仅是人类历史上最多产的数学家，还是史上最伟大的一位学者。”²

早年生活与数学天赋

每天晚饭后，欧拉把他的孩子、家仆和寄读的学生聚集在一起进行家庭敬拜，读经，有时会有讲解和讨论。

欧拉1707年出生于瑞士的巴塞尔（Basel）。他父亲致力于数学研究，同时牧养一间福音性改革宗教会，该教会强调“内在生命的重生、主内弟兄之间的关爱与活泼的信仰”。³ 欧拉坚守这些教条，信心从未 被动摇。

年轻的欧拉由他父亲在家传授数学基础知识。1720年，他考入巴塞尔大学成为一名牧师。约翰·伯努利（Johann Bernoulli）在这所大学执教数学，他也是欧拉一家的世交，后来成为欧洲最重要的数学家之一。欧拉对数学的热爱和非凡的数学才华给约翰留下深刻印象，于是他不仅给欧拉在周六下午开小灶，指导欧拉学习数学、天文学和物理学，而且还去说服他父亲欧拉的才干预定是要用于数学领域而非神学领域。

进入巴黎大奖赛

1727年，欧拉提交了一篇论文参加巴黎科学院每年举办的巴黎科学大赛——欧洲当时最著名的科学赛事。这篇论文提出了使船达到最大航速时桅杆放置的最佳方法，其中涉及桅杆的数量、位置和高度，并获得了荣誉奖。在随后的几年，欧拉两次获得荣誉奖，并在12次参赛中，他也独立获得或者与他人共同获得奖项。

在俄国的生活

从1727年到1741年，欧拉在圣彼得堡皇家科学院任教，并于1731年晋升为物理学教授，两年后被任命为数学系主任。欧拉传记的作者罗纳德·卡林格（Ronald Calinger）写道：“他的研究领域广泛，尽管其主攻方向是理论力学，但还包括了代数、算术、天文学、弹道学、圆锥曲线、微分几何、弹力、无穷级数、音乐理论、数论和振荡。由于确信数学科学是统一的，欧拉致力于对每个数学分支进行完善。”⁴

欧拉参与的实践活动还有设计消防车，向俄国海军提供建议，为俄国学校编写课本，并用德语撰写了两卷初等算术书籍。首张精确大比例俄帝国地图的制作也少不了欧拉的帮助。这份俄国地图发布于1745年，在制作过程中需要对经纬度进行精准测定。

婚姻与家庭

1734年，欧拉迎娶了凯瑟琳·格塞尔（Katharina Gsell），他们膝下有13个孩子，其中8个不幸夭折，幸存的5个孩子，仅有3个比他们的父母更长寿。卡林格写道：

每天晚饭后，欧拉把他的孩子、家仆和寄读的学生聚集在一起进行家庭敬拜，读经，有时会有讲解和讨论。在孩子临睡前，欧拉也会经常给他们朗读经文和儿童圣经故事。⁵

解决巴塞尔问题

有一道数字谜题在1644年被提出后就一直困扰着当时世界上最伟大的数学家，欧拉于1735年给出了解决方法，一举成名。这道题需要求证自然数平方倒数的精确求和，例如对以下无穷级数进行精确求和：

 

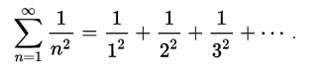
欧拉证明了当n趋向无穷大的时候，这个级数的和是π²/6。对于受过数学专业教育的读者，可以从下面网址查看这道题的（英文）证明过程：wikipedia.org/wiki/Basel_problem.

解决哥尼斯堡七桥问题

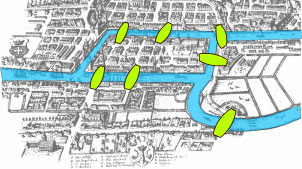
普鲁士东部的哥尼斯堡（Königsberg）旧城（今俄罗斯加里宁格勒）之前有四块陆地，由七座横跨普雷格尔河（Pregel River）的桥连接，如下图所示。

当地市民闲暇时会尝试在不重复、不遗漏的情况下，一次经过七座桥来走遍这四块陆地，最后回到出发点。

尽管没有人能做到，但看起来也没有人可以绝对否认这种走法。欧拉来了！1735年，他用大量的逻辑推理加上一点算术运算，解答了这个难题。欧拉指出：

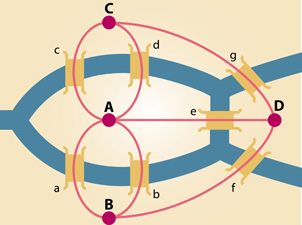
• 每块陆地内部路线的选择是无关紧要的。

• 出入每块陆地都要使用两条不同的桥。

• 所以连接每块陆地的桥的数量是偶数。

• 但是，有一块陆地有5座桥连接，另外三块陆地各自有3座桥连接。

• 所以，上述的走法无法实现。

欧拉解答哥尼斯堡七桥问题为现代图论奠定了基础，也预示了拓扑学的概念。

1738年，欧拉的右眼患了脓肿，之后视力下降，给他未来的生活带来严重影响。

在柏林的职业生涯

1741年，欧拉作为科学界和哲学领域的一位“超级明星”而备受“猎头”关注，并受邀入职柏林普鲁士皇家科学院。在那里工作的25年间，他撰写了大概380篇文章，把数学应用到一系列的学科当中。欧拉还写了两本让他最得以成名的书。一本是在1748年出版的《无穷分析引论》（Introductio in analysin infinitorum；分两卷），该书是关于函数的讨论，有可能是现代历史上最具影响力的数学教科书，另一本是1755年出版的《微积分概论》（Institutiones calculi differentialis），主要讨论微积分领域的微分学。

欧拉第三本在当时具有里程碑意义的作品是他于1749年出版的《航海科技》（Scientia navalis）。该书讨论了船舶如何设计才能使其稳定性、操作性和速度处于最佳状态——这三者在实践中常常很难彼此协调。

伯努利的赞誉

前面提到的约翰·伯努利比欧拉年长40岁，他被广泛推崇为继牛顿年迈隐退和莱布尼兹逝世后（1716年），无可争议的“数学王子”。然而，伯努利也承认欧拉这位昔日门生的才华。虽然伯努利不喜欢奉承别人，但他在信中对欧拉的问候很快上升到由衷的赞叹；1745年伯努利开始给年轻人写信，信中他写道“致无与伦比的莱昂哈德·欧拉，数学家当中的王子。”⁷

科普先驱

1759年，欧拉受邀辅导14岁的弗里德里克·夏洛特·利奥波丁·路易丝（Friederike Charlotte Leopoldine Louise），她是国王腓特烈二世的堂妹，后来成为人们熟知的普鲁士公主。为了教好这位公主，在之后两年多的时间，欧拉用清晰平白，令人信服的文字和普通人都能理解的术语给她写了234封信件，其中不涉及任何方程和公式。这一系列的信件《欧拉致德国公主的书信：关于自然哲学的不同学科》（Letters of Euler on Different Subjects in Physics and Philosophy Addressed to a German Princess）发表在圣彼得堡科学院（第1、2卷在1768年发表，第3卷发表在1772年）。

这些书信的法语第二版在欧拉逝世后的1787年到1789年间在巴黎发表。这个版本由伏尔泰（Voltaire）的学生，尼古拉斯·德·孔多塞（Nicolas de Condorcet）担任编辑。他对欧拉在文中提及到上帝和亚当夏娃（表明欧拉相信创世记是真实历史）感到不满，故意把相关段落删除掉。但是，英文版的编辑亨利·亨特（Henry Hunter）有意把大部分被删减的文字在该套书信1795年的英文版中补回来。

卡林格把这些书信形容为“18世纪最详尽和最权威的科普作品。”⁸ 书信讨论的主题包括重力、潮汐、太阳系、牛顿运动定律、声、光、电、磁的属性、大气、冷热、炮弹轨道等诸多领域。欧拉还解释了诸如温度计、望远镜和显微镜等科学仪器，还有眼睛结构和视觉等。欧拉还教了这位弗里德里克公主逻辑，为此他用了三段论的图表（见第35页方框）。

在若干封信件中，欧拉向公主介绍了他关于上帝、祷告、永生、邪恶与罪、神的审判、逆境的益处和罪人回转等方面的看法。他在41号信件解释了眼睛的精妙：

虽然我们还远远未能明白（眼睛）这个领域的完整知识，但目前所掌握的为数不多的知识足以让我们确信创造者的大能和智慧。我们发现眼球的完美结构，这是最伟大的天才都未曾想象到的。⁹

弗里德里克公主肯定是世界上最博学的年轻人，她鼓励把这些书信发表出来，惠及大众。截止到1800年，这些书信被翻译成8种语言，发表了30个版本。

返回圣彼得堡

欧拉1766年回到圣彼得堡，接受当地皇家科学院提供的一个职位。数月之后，他发高烧，左眼也随之出现问题，导致视觉严重丧失。卡林格写道：

即使在几乎失明的情况下，欧拉惊人的记忆、丰富的想象力、坚定的意志力量、永不满足的好奇心以及训练有素的直觉继续为他保驾护航，沉醉于科学研究和解决最难问题的愉悦使他就视力问题自信地说“又一令我分心的东西被拿走了”。¹⁰

欧拉的记忆力惊人，他能背诵维吉尔（Virgil）的《埃涅阿斯纪》（Aeneid），可以指出每一页开头是哪句诗，结尾是哪句诗。¹¹

他非凡的文字创造力非但没有受不断恶化的视力问题影响，相反还在与日俱增。“作为主要作者，或者是整个印刷流程的督导，欧拉主持了一系列文章和书籍的发行，数量多达415种……他逝世的时候，还有超过150种尚未面世。”¹²

这时候，欧拉又完成了另一本畅销书：备受赞誉，厚达500页的《代数完全指南》（Complete Guide to Algebra）。在1773年，欧拉完成了他最后一部重要著作——他航海论文的简化版：《海员应会的船舶建造与操作的完整理论》（Complete theory of the construction and maneuver of ships brought into the reach of everyone involved in navigation）。这本书覆盖了水手必需掌握的船只运动知识，书中的语言是水手、航海家、桅杆制造商和造船商都能轻易读懂的。

欧拉因中风后的各种并发症于1783年逝世。

致敬欧拉

卡林格写道：

科学界意识到失去了一位杰出的同事：分布伦敦、巴黎、柏林和圣彼得堡的四所皇家科学院，以及坐落在巴塞尔、里斯本、慕尼黑、斯德哥尔摩和都灵的学会，也就是欧拉生前所在的机构，都宣告了他们这一重大损失。¹³

在他生命的尽头，所有欧洲数学家都将他视为他们的老师。

圣彼得堡科学院保存有大量欧拉未曾发表的作品，在欧拉逝世之后陆续发表了近50年。自1911年，瑞士科学院就开始发布《欧拉全集》（Opera Omnia）。迄今（2017年），已经有72卷（四开本）面世，其中3个系列分别涵盖了数学、力学、天文学和杂文，共计约35000页。第4个系列有10卷，含欧拉现存的3300封书信，他以法语、拉丁语、德语、俄语和部分以英语写给了275位记者，这个系列目前还在出版中。

欧拉的头像还出现在瑞士、俄国、德国和其他国家的邮票和瑞士面值为10法郎的纸币上。为了致敬欧拉，天文学家用他的名字来命名月球上的一个陨石坑和一颗小行星。温柔和谦卑的欧拉是当时最伟大的数学家——自他逝世后直到19和20世纪，全欧洲的数学家都把欧拉视为老师。比如，杰出的法国数学家皮埃尔·西蒙·拉普拉斯（Pierre Simon Laplace，1749-1827）曾经说：“读欧拉；读欧拉；他是我们众人的大师！”¹⁴ 欧拉是一位完全委身、尊敬上帝和相信圣经的基督徒。 

 

欧拉对当今数学的影响

许多今天使用的数学术语和记号都是由欧拉创立、推广和标准化，包括：
• f(x)表示函数
• x、y、z表示未知数
• a、b、c表示三角形的边
• A、B、C表示对顶角
• R和r表示三角形外接圆和内接圆的半径
• 三角函数的缩写sin、cos、tan、csc、sec、cot
• π的推广使用（并非是欧拉首创）
• ∑是求和记号
• Δ有限差分
• i是虚数√-1的单位
• e是自然对数的底，e ≈ 2.71828
• 压杆临界力的欧拉公式：P_cr = π²EI/(KL)²
• 欧拉公式 eⁱπ= –1，也称为欧拉身份的象征（现代形式为e^iπ+ 1 = 0），数学家赞扬“它是数学界其中一个最美丽的公式”，因为这个公式包含了很多元素，比如五个最重要的数学常数出现在这个公式中。
• 欧拉多面体公式也称为欧拉示性数：V-E+F=2 (这里的V代表顶点的数量，E代表棱的数量，F代表简单的三维凸多面体（没有孔）的面的数量)

更多信息，请访问：en.wikipedia.org/wiki/List_of_things_named_after_Leonhard_Euler. 

  

欧拉教导逻辑时使用的图表

欧拉的一项鲜为人知的发明就是他用三段论的图表向弗里德里克公主教导逻辑。他从103号信第398页第一次这样做，并将其应用到各种假设情况，直到108号信为止。自1960年以来，欧拉图（现在的叫法）与韦恩图（约翰·韦恩John Venn c.于1880年构想出来的，它是欧拉图重叠时的一种特殊情况）一起被用来说明集合中不同元素之间的关系。重点不是曲线的大小或形状，而是它们是如何重叠的。完全包含在另一条曲线中的曲线表示它是该曲线的一个子集。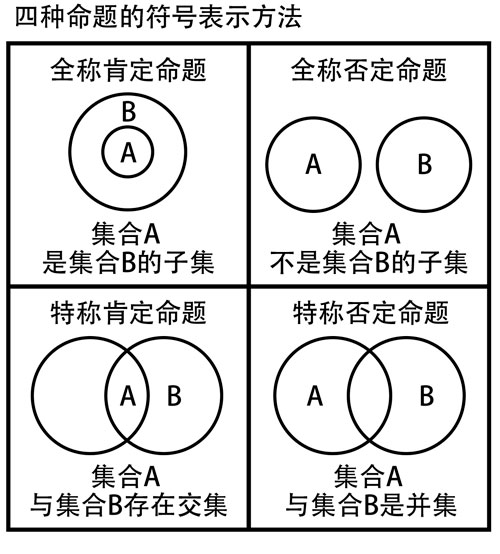
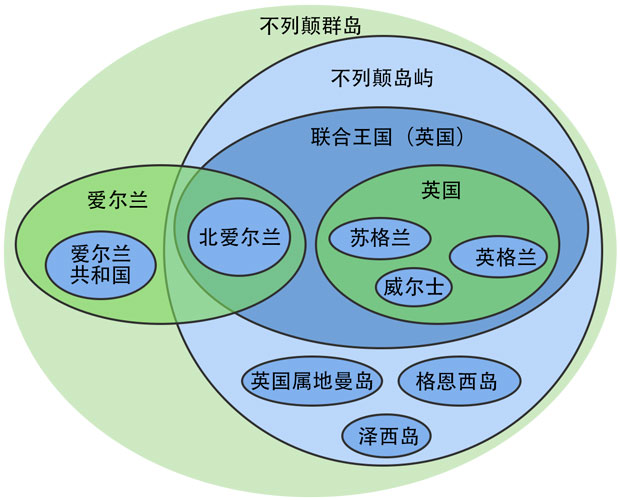	写给弗里德里克公主的103号信件中，欧拉用来教导逻辑的图表	不列颠群岛的欧拉图（来自维基百科）

 

   

【扩展阅读】

● 科学坚固对上帝的信心

● 奥康姆的威廉——第一位新教徒

● 了不起的罗伯特·菲兹罗船长：气象学的先驱

● 进入创世真理的超强引力场

● 创造伉俪

● 会见非凡的一家——他们都信创造论

● 现代科学发源于圣经

 

---